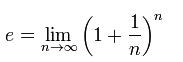Destina
FK Üyesi
-
- Katılım
- 1 May 2020
-
- Mesajlar
- 938
-
- Tepkime puanı
- 1,286
-
- Puan
- 93
-
- Web sitesi
- forumderyasi.com
Euler Sayısı Nedir? Nasıl Bulundu?
“e” sayısı matematikte ve mühendislik biliminde çok önemli bir yere sahip, sıkça kullanılan sabit bir reel sayıdır. Doğal logaritmanın tabanıdır ve ayrıca irrasyoneldir.
Pi sayısının yanında daha gizemli görünen e sayısı adını ünlü matematikçi Euler’in baş harfinden alır. Bir diğer ismi de "Euler sabiti"dir.
Yaklaşık değeri;
e= 2.718281828459045235360287471352662497757247...
Bu sayıya ilk olarak İskoç matematikçi John Napier değinmiş fakat üzerinde durmamıştır. Sadece logaritma ile ilgili yayınladığı bir ekinde hafifçe bahsetmiştir. Bunun üzerine gerçek anlamda bu sayıyı ilk bulan kişi ise İsviçreli matematikçi Jakob Bernoulli’dir.
Peki Bernoulli Bu Sayıyı Nasıl Buldu?
"e" sayısının bulunuşu 17. Yüzyılların ilk başlarına dayanıyor. O dönemde coğrafi keşiflerinde etkisiyle uluslararası ticarette ve finansal işlerde büyük bir artış olmuş, bileşik faiz fikri daha çok ilgi çekmeye başlamıştı. Jakob Bernoulli e sayısını bir bileşik faiz probleminden buldu.
Problemden bahsedecek olursak;
Örneğin 100 TL paramız olduğunu düşünelim. Bir banka yıllık %5 bileşik faizde bankaya yatıracak olursak bir yılda paramız 105 TL olur. İkinci yılda 105*1,05 olur. Her yıl yeni fiyattan faiz işler ve para gittikçe büyür.
Şimdi de 1 TL paramız olduğunu düşünelim;
► Yılda %100 faiz veren bir bankaya yatırırsa 1 sene sonra 2 lirası olur.
► 6 ayda bir %50 faiz veren bir bankaya yatırırsa 1 sene sonra 2,25 lirası olur.
► 3 ayda bir %25 faiz veren bir bankaya yatırırsa 1 sene sonra 2,44... lirası olur.
► Ayda bir %8,33... faiz veren bir bankaya yatırırsa 1 sene sonra 2,6130... lirası olur.
► Ve aynı şekilde haftada bir işleyen faiz sonunda 1 sene sonra 2,6925... lirası olur.
► Her gün işleyen faizi hesapladığımızda ise 1 sene sonra 2,71453... lirası olur.
Bunu formülize edecek olursak;
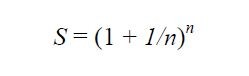
► "n" için küçük değerler verecek olursak;

► "n" için büyük değerler verecek olursak;

►Faiz süresini kısalttığımızda e sayısına daha da yaklaşmış oluruz. n sayısının sonsuzda limitini aldığımızda e sayısı bu şekilde ifade edilir;
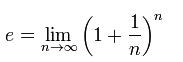
“e” sayısı matematikte ve mühendislik biliminde çok önemli bir yere sahip, sıkça kullanılan sabit bir reel sayıdır. Doğal logaritmanın tabanıdır ve ayrıca irrasyoneldir.
Pi sayısının yanında daha gizemli görünen e sayısı adını ünlü matematikçi Euler’in baş harfinden alır. Bir diğer ismi de "Euler sabiti"dir.
Yaklaşık değeri;
e= 2.718281828459045235360287471352662497757247...
Bu sayıya ilk olarak İskoç matematikçi John Napier değinmiş fakat üzerinde durmamıştır. Sadece logaritma ile ilgili yayınladığı bir ekinde hafifçe bahsetmiştir. Bunun üzerine gerçek anlamda bu sayıyı ilk bulan kişi ise İsviçreli matematikçi Jakob Bernoulli’dir.
Peki Bernoulli Bu Sayıyı Nasıl Buldu?
"e" sayısının bulunuşu 17. Yüzyılların ilk başlarına dayanıyor. O dönemde coğrafi keşiflerinde etkisiyle uluslararası ticarette ve finansal işlerde büyük bir artış olmuş, bileşik faiz fikri daha çok ilgi çekmeye başlamıştı. Jakob Bernoulli e sayısını bir bileşik faiz probleminden buldu.
Problemden bahsedecek olursak;
Örneğin 100 TL paramız olduğunu düşünelim. Bir banka yıllık %5 bileşik faizde bankaya yatıracak olursak bir yılda paramız 105 TL olur. İkinci yılda 105*1,05 olur. Her yıl yeni fiyattan faiz işler ve para gittikçe büyür.
Şimdi de 1 TL paramız olduğunu düşünelim;
► Yılda %100 faiz veren bir bankaya yatırırsa 1 sene sonra 2 lirası olur.
► 6 ayda bir %50 faiz veren bir bankaya yatırırsa 1 sene sonra 2,25 lirası olur.
► 3 ayda bir %25 faiz veren bir bankaya yatırırsa 1 sene sonra 2,44... lirası olur.
► Ayda bir %8,33... faiz veren bir bankaya yatırırsa 1 sene sonra 2,6130... lirası olur.
► Ve aynı şekilde haftada bir işleyen faiz sonunda 1 sene sonra 2,6925... lirası olur.
► Her gün işleyen faizi hesapladığımızda ise 1 sene sonra 2,71453... lirası olur.
Bunu formülize edecek olursak;
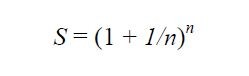
► "n" için küçük değerler verecek olursak;

► "n" için büyük değerler verecek olursak;

►Faiz süresini kısalttığımızda e sayısına daha da yaklaşmış oluruz. n sayısının sonsuzda limitini aldığımızda e sayısı bu şekilde ifade edilir;